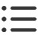职测数量关系中,计算问题是常考的一类问题,而在计算问题中又经常会涉及到不定方程的考查。这类题目看似复杂,其实难度较低,只需要结合系数的特点就能快速解决。今天,金标尺就带大家一起来学习一下。
一、不定方程的定义
1.不定方程:未知数的个数多于独立方程个数的方程或方程组。
2.独立方程:表达同一个方程式的称为同一个独立方程。例如 
![]() ,称为同一个独立方程。
,称为同一个独立方程。
二、常见应用
1.倍数特性:适用于未知数系数与常数项存在公因数。
【例1】8x+13y=120,已经x和y均为正整数,则y为多少?
A.6
B.7
C.8
D.9
【金标尺解析】C。观察等式左右两边,可发现120与8存在公因数8,120是8的倍数,8x也是8的倍数,x和y都为正整数,可得13y也应是8的倍数,而13不是8的倍数,那么y必定是8的倍数,即能够被8整除,观察选项只有C选项能够被8整除,故本题答案为C项。
2.奇偶特性:适用于未知数的系数一奇一偶。
【例2】办公室工作人员使用红、蓝两种颜色的文件袋装29份相同的文件。每个红色文件袋可以装7份文件,每个蓝色文件袋可以裝4份文件。要使每个文件袋都恰好装满,需要红色、蓝色文件袋的数量分别为( )个。
A.1、6
B.2、4
C.4、1
D.3、2
【金标尺解析】D。设红色文件袋x个,蓝色y个,依据题意得,7x+4y=29,由奇偶性可知,4y为偶数,29为奇数,则7x必为奇数,即x必为奇数,排除B、C项。代入A项,7×1+4×6≠29,排除,故本题答案为D项。
【例3】把69瓶矿泉水装入盒子里,现有两种盒子,大盒每盒装8瓶,小盒每盒装5瓶,要求每个盒子都恰好装满,共用了十多个盒子刚好装完,则需要大、小盒子各多少个?
A.3、8
B.8、4
C.3、9
D.4、9
【金标尺解析】C。由题意可知,设有x个大盒,y个小盒,列出8x+5y=69。观察未知数前的系数一奇一偶,可以考虑用奇偶特性,8x一定为偶数,69为奇数,则5y一定是奇数,y为奇数,排除A、B项;当y=9时,解得x=3。故本题答案为C项。
通过上述几题的练习,相信大家对于不定方程的常见考点以及解题方法都有了初步认识,后面还需要多多做题,才能熟能生巧,熟练掌握不定方程的各类解题方法。