地区

职测数量关系中极值问题一直是高频考点，这类题计算量少，题型简单易识别，好拿分，在考场上一定不要放过。今天金标尺就和大家分享极值问题中常考题型之一——一元二次函数，相信各位考生在学习后，都能快速识别并解决这类问题。接下来大家一起来跟金标尺学习吧!

一、一元二次函数的题型特征

某类题目所求的量可以用形如一元二次函数：y=ax²+bx+c（a≠0）的式子表示出来并求其极值。例如：利润极值问题，几何问题等等。

二、一元二次函数的解题方法

①当x=时，y取得极值；②令y=0，解得x₁和x₂，当x=时，y取得极值。

下面让我们通过这几道题练习一下吧！

【例1】某超市出售一箱矿泉水，如果以每瓶4元出售，可卖出2000瓶；若矿泉水每提高1元，就会少卖100瓶。则在最佳定价的情况下，该超市最大收入为（   ）元。

A.10000

B.12000

C.14400

D.16000

【答案】C。解析：设该超市收入为y元，矿泉水提高了x元，少卖100x瓶。法一：y=（4+x）（2000-100x）=-100x²+1600x+8000，当x==8时，y取得最大值，为（4+8）×（2000-100×8）=14400元，故本题答案为C项；

法二：y=（4+x）（2000-100x），令y=0，解得x₁=-4和x₂=20，当x==8时，y取得最大值，为（4+8）×（2000-100×8）=14400元。故本题答案为C项。

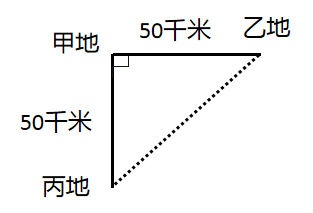
【例2】甲地在乙地正西50千米外，在丙地正北50千米外。A、B两辆汽车分别从乙地和丙地同时出发，分别以50千米/小时和60千米/小时的速度向正西和正北行驶。问出发多长时间后，两辆车之间的距离最短?（   ）

A.不到50分钟

B.50～55分钟之间

C.55～60分钟之间

D.60分钟以上

【答案】B。解析：根据题意作示意图如下。设出发的时间为x小时，两车的距离为y千米。那么出发后x小时A车距离甲地（50-50x）千米，B车距离甲地（50-60x）千米。根据勾股定理可得，则根据一元二次函数的性质可得在=时，y取得最小值。小时≈54.5分钟，在B项范围内。故本题答案为B项。

 

总结：相信学到这儿时，大家都清楚地掌握了一元二次函数的解法。同学们记得平时要多练习，才能融会贯通~