近年来，职测数量关系越来越重视几何板块的考查，这类题往往具有一定难度，常常是考试中拉开分差的关键。今天金标尺就和大家分享几何问题中常考题型之一--相似三角形，相信各位考生在学习后，都能快速识别并解决这类问题。接下来大家一起来跟金标尺学习吧!
一、相似三角形的性质
1.对应边长/高/周长=相似比；
2.面积之比=相似比的平方。
二、相似三角形的判定
1.平行于三角形一边的直线和其他两边或两边的延长线相交，所构成的三角形与原三角形相似；
2.如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似（两边对应成比例且夹角相等，两个三角形相似）；
3.如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似（三边对应成比例，两个三角形相似）；
4.如果两个三角形的两个角分别对应相等（或三个角分别对应相等），则有两个三角形相似（两角对应相等，两个三角形相似）。
三、相似三角形的模型
【模型一】A字形
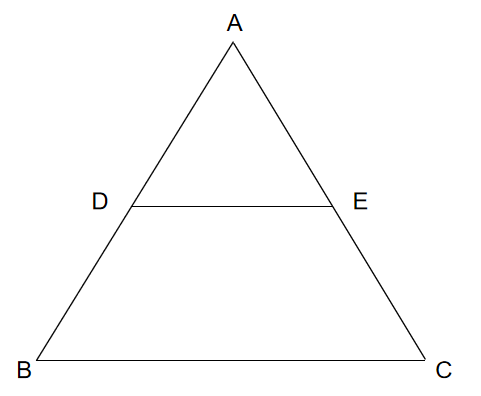
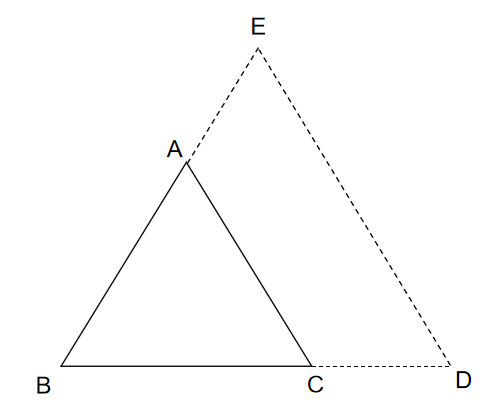
结论：有两个角对应相等或两边对应成比例且夹角相等的两个三角形相似．
【模型二】8字形
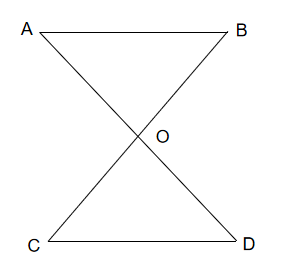
结论：有两个角对应相等或两边对应成比例且夹角相等的两个三角形相似。
【模型三】双垂线形
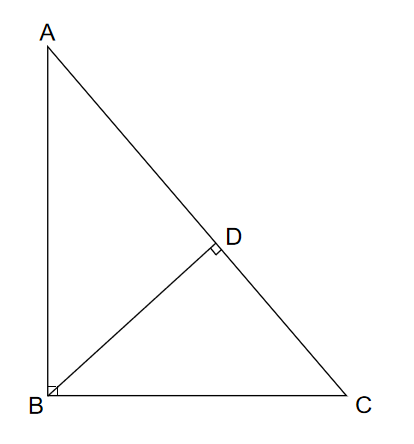
结论：有两个角对应相等或两边对应成比例且夹角相等的两个三角形相似．
下面让我们通过这几道题练习一下吧！
【例1】如图，直角三角形ABC中，∠C=90︒，AC=8厘米，BC=6厘米，正方形CDEF的顶点D、E、F在三角形的边上，求正方形的边长为多少厘米？
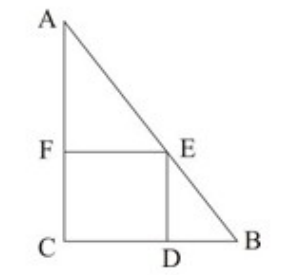
A.3
B.24/7
C.4
D.24/5
【金标尺解析】设正方形边长为x，由“A字模型”可知，△AEF∽△ABC，根据相似图形对应边成比例可得：
，即
，解得x=24/7。故本题答案为B项。
【例2】一块种植花卉的矩形土地如图所示，AD边长是AB的2倍 ，E为CD边的中点， 甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地面积的：
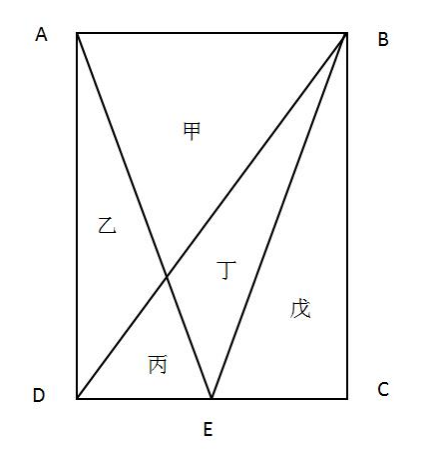
A.3/4
B.2/3
C.7/12
D.1/2
【金标尺解析】种植白花的区域为甲和戊，由“8字模型”可知，甲、丙为相似三角形，根据E为DC中点可得
，又由于甲高+丙高=AD，所以甲高为
，戊为底边为CE，高为BC的直角三角形，则种植白花的面积=甲的面积+戊的面积=
，占矩形土地面积的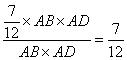
。故本题答案为C项。
总结：相信学到这儿时，大家都清楚地掌握了相似三角形的做题方法。同学们记得平时要多多练习，才能融会贯通~
